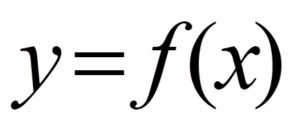Функция – выражает зависимость между переменными величинами, при которой каждому рассматриваемому значению одной величины Х соответствует определённое значение другой величины Y. При этом Х называется аргументом, или независимой переменной (поскольку её значения заданы), а Y – функцией, или зависимой переменной (поскольку она зависит от Х). Соотношение между Х и Y в общем виде записывается так: \( y=f(x) \). Иными словами, понятие функции выражает идею действия, которое необходимо совершить над одной величиной, чтобы получить другую. В связи с этим в технических дисциплинах функция определяется как устройство, на входе которого подается х, а на выходе возникает у. Ключевое слово в понятии функции – зависимость или взаимосвязь.
Функцию можно задать тремя способами:
- Аналитический – с помощью формул;
- Табличный – с помощью таблиц, где можно указать значения функции, однако лишь для конечного набора значений аргумента;
- Графический – способ задания функции очень удобен: он дает возможность наглядно представить свойства функции.
Наиболее привычным является представление функции в виде формулы: \( y=sin(x) \), \( y=2x+3 \) и т.д. Некоторые функции представлены в виде таблицы. Этот способ является единственно возможным в том случае, если зависимость устанавливается экспериментально, при этом формула еще не выведена, а график не построен.
Графики необходимы тогда когда невозможно быстро и качественно обрабатывать большие объемы однотипной информации, представленной в текстовой форме. Такую информацию гораздо удобнее обрабатывать с помощью таблиц. Но восприятие громоздких таблиц также оказывается затруднительным для человека. График позволяет отслеживать динамику изменения данных.
На графике видно, например, что функция непрерывна на некоторых промежутках, видны промежутки ее возрастания и убывания, экстремумы, поведение в бесконечности, в особых точках. Другими словами, график функции можно использовать как геометрическую иллюстрацию, интерпретацию свойств функции.